Сценарій відео: "Що таке модуль числа?"
(Вступ)
Привіт! Сьогодні ми розберемося з однією з найцікавіших тем у математиці — модулем числа. І допоможуть нам у цьому наші герої та звичайна координатна пряма.
(Частина 1: Про напрямок)
Подивіться на перший малюнок. Уявіть, що будинок — це наша точка відліку, число $0$.
Андрій та Марія вийшли з дому одночасно, але пішли в різні боки. Андрій попрямував праворуч і зупинився в точці $+5$. Марія пішла ліворуч і зупинилася в точці $-5$.
Числа $+5$ та $-5$ кажуть нам, де саме зараз перебувають діти відносно будинку. Плюс — це праворуч, мінус — це ліворуч.
(Частина 2: Про відстань)
А тепер запитання: а яку відстань подолав кожен із них?
Андрій зробив 5 кроків. А Марія? Вона теж зробила 5 кроків! Хіба ми можемо сказати, що вона пройшла «мінус 5 метрів»? Звісно, ні. Відстань не буває від’ємною.
(Частина 3: Нові герої — Олег та Софія)
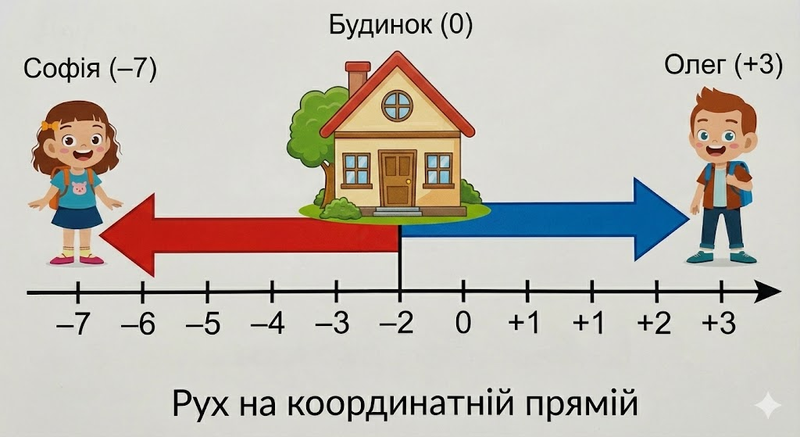
Погляньмо на другий приклад. Тут у нас Олег та Софія.
Олег пройшов праворуч і опинився в точці $+3$. Його шлях — це 3 одиничні відрізки.
Софія пройшла ліворуч аж до позначки $-7$. Хоча вона стоїть у «від’ємній» зоні, вона пройшла шлях довжиною в $7$ одиниць.
(Частина 4: Визначення модуля)
Ось цю відстань від нуля до точки в математиці і називають модулем числа.
Запам’ятайте: модуль — це відстань. Йому байдуже на напрямок, йому важливо лише «скільки кроків зроблено».
(Частина 5: Як це записувати)
Для модуля ми використовуємо спеціальні «стіни» — дві вертикальні риски.
Подивіться, як ми запишемо шлях Софії:
$|-7| = 7$
Ми читаємо це так: «Модуль числа мінус сім дорівнює семи». Тобто відстань від нуля до мінус семи — це сім одиниць.
А шлях Олега запишемо так:
$|3| = 3$
Відстань від нуля до трійки — це три одиниці.
(Підсумок)
Отже, головне правило: модуль числа ніколи не може бути від’ємним. Це просто довжина шляху від нуля до потрібної нам точки.
Все просто: модуль «з’їдає» мінус, тому що відстань завжди додатна!



Сценарій: Як розв'язати рівняння $|x| = 3$
(Вступ)
Тепер, коли ми знаємо, що модуль — це відстань, давайте розв’яжемо наше перше рівняння: $|x| = 3$.
На перший погляд, воно виглядає незвично. Але давайте «перекладемо» його з математичної мови на нашу «мову кроків».
(Крок 1: Переклад)
Запис $|x| = 3$ означає: «Якесь число $x$ знаходиться на відстані трьох кроків від нашого будинку (точки $0$)».
Наша задача — знайти, в яких саме точках може стояти людина, якщо ми точно знаємо, що вона пройшла від дверей рівно 3 одиниці.
(Крок 2: Пошук варіантів)
Давайте подивимося на координатну пряму. У нас є два варіанти, куди можна було піти від будинку:
- Варіант перший: праворуч. Якщо ми зробимо 3 кроки праворуч, то опинимося в точці $+3$. Перевіримо: чи дорівнює модуль трійки трьом? Так! $|3| = 3$. Отже, перший корінь рівняння — це число $3$.
- Варіант другий: ліворуч. Але ж ми могли піти і в інший бік! Якщо зробити 3 кроки ліворуч, ми потрапимо в точку $-3$. А який модуль у числа $-3$? Правильно, теж $3$, бо це та сама відстань. Отже, число $-3$ — це наш другий корінь.
(Крок 3: Висновок і запис)
Виходить, що наше рівняння має одразу два розв’язки!
Адже і точка $3$, і точка $-3$ знаходяться на однаковій відстані від нуля.
Записуємо це так:
$x = 3$ або $x = -3$.
(Важливе зауваження)
А тепер підступне питання: а чи може бути таке рівняння: $|x| = -2$?
Давайте «перекладемо»: «Відстань від будинку до точки дорівнює мінус два кроки». Хіба таке буває? Звісно, ні! Відстань не може бути від’ємною.
Тому, якщо ви бачите, що модуль дорівнює від’ємному числу, сміливо кажіть: «Рівняння не має розв’язків!»
(Завершення)
Отже, запам'ятайте:
- Якщо модуль дорівнює додатному числу — шукайте два варіанти (з плюсом і з мінусом).
- Якщо модуль дорівнює нулю — відповідь тільки одна (нуль).
- А якщо модуль дорівнює від’ємному числу — розв’язків просто не існує.

